A primer on hybrid Merkle trees
Devised in the late seventies by Ralph Merkle, hash trees (nowadays commonly known as Merkle trees) allow a party to commit to a potentially long list of values in a very succinct way, and later on prove to any other party that a particular value was at a concrete position of the original list - also succinctly. This primitive turns out to be immensely useful in a variety of contexts, including modern proof systems. However, technical obstacles arise when a proof system relying on Merkle trees is made recursive, a technique which is becoming more and more widespread in SNARKs and STARKs.
In this post, we briefly recall the fundamentals of Merkle trees, present their associated difficulties in the recursive context and introduce a common approach to tackling the issue: hybrid Merkle trees (while not standard, this terminology is quite descriptive). Finally, we go over a recent Plonky3 PR which implements such trees. The latter is joint work by the author and César Descalzo.
0: Merkle-tree refresher
Let us devote a few lines to recalling how hash trees operate, which can be safely skipped by readers familiar with the topic. Let $\mathcal{P}$ be a party, which we will refer to as the prover, holding a list of values $v_1, \ldots, v_n$ from some value space $S$. The only cryptographic tool needed to construct the Merkle tree is a compression function $C \colon S \times S \to S$. The basic algorithms to commit to the list, open a particular value and verify such an opening are as follows:
$\mathsf{Commit}((v_i)_{i = 1}^n) \to r, n$:
Convert $(v_i)_{i = 1}^n$ into a list $[v_1, \ldots, v_n]$ (which cannot be empty) and set the length $l$ to the initial value $n$.
While $l > 1$:
From left to right, replace each contiguous pair of values $(v_{2k - 1}, v_{2k})$ (with $1 \leq k \leq \lfloor k/2 \rfloor$) by its compression $C(v_{2k - 1}, v_{2k})$. If $l$ is odd, the last element $v_l$ remains untouched. Relabel the elements of the resulting list as $v_1, v_2, \ldots$.
Set $l = \left\lceil k/2 \right\rceil$ (the length of the current list).
Output $r := v_1$ and $n$.
The lists across the iterations of the loop form the levels of a binary tree with root $r$ where each node is the compression of its two children (except for the leaves and the final nodes of odd-length levels). This tree can be stored by the prover at commit time (constituting a so-called opening hint) or re-computed at opening time from the full list of values (which is substantially less efficient, especially if many values are to be opened). We assume the former and denote the tree by $T$, which looks as follows:
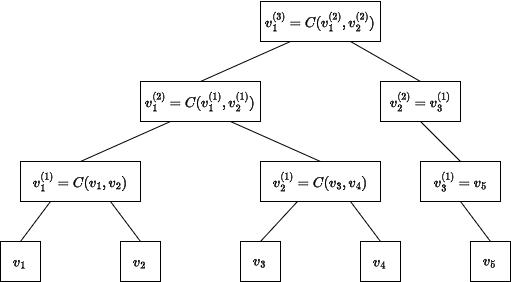
Committing work is linear in $n$: $C$ is called $n - 1$ times.
Suppose $\mathcal{P}$ committed to the list $(v_i)_{i = 1}^n$ as above by sharing $r$ and $n$ with another party, which we call the verifer $\mathcal{V}$, and now wishes to open the $i$-th element of the list.
$\mathsf{Open}(T, i) \to v_i, s$:
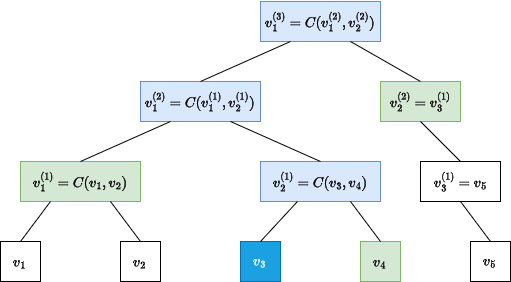
- Let $p$ be the path from the $i$-th leaf $v_i$ of $T$ to its root. Construct the list $s$ containing each sibling of each node in $p$ (in order). For nodes without a sibling, do not include anything in the list.
- Output $v_i, s$.
In the following diagram, the opened node $v_i = v_3$ is dark blue, the path $p$ to the root is light blue, and the siblings $s$ included in the proof are light green:
$\mathsf{Verify}(r, n, i, v, s) \to \mathsf{accept} \ \text{or} \ \mathsf{reject}$:
While $n > 1$:
If $n$ is even or $i \neq n$:
- Pop the first element from $s$, denote it by $f$.
- Update $v$ to $C(v, f)$ if $i$ is odd and to $C(f, v)$ otherwise.
Update $n = \left\lceil n/2 \right\rceil$ and $i = \left\lceil i/2 \right\rceil$.
$\mathsf{accept}$ if $v = r$, otherwise $\mathsf{reject}$.
The idea of verification is for $\mathcal{V}$ to reconstruct the path from the purported leaf $v$ to the committed root $r$ using the compression function. The indices $n$ and $i$ allow the verifier to keep track of which order to compress pairs in, as well as detect steps where no compression should happen (because the current node is the final one of an odd-length level).
The verification cost is logarithmic in $n$, since one call to $C$ is made per level of the tree (except at the leaves).
Security
Although an explanation of security is not this post’s aim and no formal definitions or proofs will be given, it is worth having some intuition of which guarantees one expects from the Merkle-tree construction and how to achieve them, which we now devote a few lines to.
As a commitment scheme, Merkle trees should above all be binding: once the prover shares $r$ and $n$ with the verifier, they should not be able to produce (valid) opening proofs of two different values $v_i \neq \tilde{v}_i$ at the same index $i$. Suppose that $\mathcal{P}$ were able to do so, and let $s$ and $\tilde{s}$ be the respective lists of siblings provided as part of the proofs. Define $p$ and $\widetilde{p}$ to be the list of values obtained by compressing pairs of values as indicated by the verification algorithm (taking into account the directionality dictated by $i$) - that is, the paths reconstructed by the verifier. Since both proofs are accepting with respect to the same commitment, which includes the root $r$, the paths start at different values $v_i \neq \tilde{v}_i$ and end at the same one $r$. Let $o$ be the first value at which they coincide. The prover therefore knows two different pairs of values $(a, b) \neq (c, d)$ such that $C(a, b) = C(c, d) = o$ (note that not all nodes in the tree are the output of $C$ due to odd-length levels, but an uncompressed node could never be the first coincidence of the $p$ and $\widetilde{p}$ - can you see why?).
It follows that, in order to break the binding property, a dishonest prover would need two distinct preimages of the same value $o$ under $C$. Note that $C$ cannot be injective by a trivial cardinality argument (since $S$ is finite), but finding two values mapped to the same image should be computationally infeasible. This strongly hints at the right type of mapping to use as $C$: cryptographic hash functions, or at least functions satisfying collision resistance.
A slightly subtler point which we have implicitly stressed (which is admittedly a bit of an oxymoron) is that the number $n$ of committed values should be a part of the commitment itself, and hence made available to the verifier. A failure to do so opens the door to a very simple type of attack: suppose the prover builds a tree $T$ honestly from the list of values $v_1, \ldots, v_n \in S$, with $n$ even, and shares the root $r$ with the verifier. Later on, they can honestly open $v_{n - 1}$ and $v_n$ by sharing their values, the corresponding index, and the length $n$ (together with the opening proof). However, they can also claim that the original list had length $n - 1$ and open the (dishonest) value $\tilde{v}_{n - 1} = C(v_{n - 1}, v_n)$ by providing the siblings of the path in a “trimmed” tree where the original last two leaves have been cut off. In a way, sharing $n$ as part of the commitment binds the prover to the structure of the tree and prevents this attack and other similar ones.
1: Hybrid Merkle trees
Motivation
Hybrid Merkle trees are a variant of the above scheme where more than one compression function $C$ is used across the various levels of the tree. For reasons that will become clear soon, the applicability of this is mainly limited to recursive proof systems, where the prover $\mathcal{P}$ does not directly send a proof $\pi$ to the verifier $\mathcal{V}$ for checking, but instead produces a second proof $\pi_{\mathcal{V}}$ that a circuit $L_{\mathcal{V}}$ encoding $\mathcal{V}$’s verification logic has successfully checked $\pi$. It is then $\pi_{\mathcal{V}}$ that gets sent to the other party for actual verification. The motivation for this paradigm usually lies in the different strengths of various proof systems, which allow one to tweak the balance between prover time, verifier time and proof size (as well as other metrics) by selecting suitable inner (think $\mathcal{V}$) and outer (think $L_{\mathcal{V}}$, or the actual verifier) proof systems.
As far as Merkle trees are concerned, the main complication introduced by recursion is that circuits such as $L_{\mathcal{V}}$ are usually defined in terms of the arithmetic of some finite field other than $\mathbb{F}_2 = \{0, 1\}$. These fields are generally poorly suited to capture the bitwise operations (such as XOR and shifts) that underpin the state-of-the-art hash functions (e. g. SHA256, Blake3). This results in significantly downgraded performance of Merkle path verification circuits for trees built with such hashers. In order to avoid this, one can switch to so-called arithmetic hash functions, which are defined in terms of finite-field operations (addition, multiplication, inversion) and therefore have much more flattering runtimes when executed inside arithmetic circuits than bit-based ones. Families of such functions include Poseidon, Rescue and Vision. However, arithmetic hashes come at a cost: native performance (that is, when running procedurally, outside a circuit) is typically orders of magnitude worse than that of bit-based hashes. This native cost will be incurred by the prover when constructing the tree (i. e. committing), which is already a costly operation. This means that switching to arithmetic hashes is not an ideal solution either… at least in isolation.
The hybrid strategy
The tension between bit-based and arithmetic hash functions - or equivalently, between native and in-circuit performance, - can be resolved by leveraging the asymmetry in the work performed by the prover and the verifier. Indeed:
- When constructing a tree with $n = 2^l $ leaves, the prover calls the compression function $2^l - 1$ times natively.
- When recursively proving or verifying a path, the circuit calls the hash function $l$ times (this costs can affect both $\mathcal{P}$ and $\mathcal{V}$).
Consider two different hash functions $C_1, C_2 \colon S \times S \to S$ and denote their native and in-circuit execution costs by $ t_1^{(n)}$, $ t_2^{(n)}$, $ t_1^{(r)}$ and $ t_2^{(r)}$, respectively. Suppose that, instead of employing $C_2$ all throughout, the prover were to switch to $C_1$ when compressing the leaves and use $C_2$ only when compressing all subsequent levels up to the root. Then:
- The commitment cost changes from $2^l - 1$ calls to $C_2$ to $2^{l - 1}$ calls to $C_1$ plus $2^{l - 1} - 1$ calls to $C_2$.
- The in-circuit (recursive proving and final verification) cost changes from $l$ calls to $C_2$ to 1 call to $C_1$ plus $l - 1$ calls to $C_2$.
In other words:
By switching from an arithmetic hash function $C_2$ to a bit-based one $C_1$ at the bottom level, the prover saves work in about half of all the hashing performed natively, whereas in-circuit proving and verification costs only increase on a $1/l$-fraction of the hashing.
In table form, the situation is as follows:
| $\mathsf{Commit}$ (native) | $\mathsf{Open}$ and $\mathsf{Verify}$ (recursive) | |
|---|---|---|
| $\ $ | ||
| Single hash $C_2$: | $(2^l - 1) \cdot t_{2}^{(n)}$ | $l \cdot t_{2}^{(r)}$ |
| $\ $ | ||
| Hybrid hash $(C_1, C_2)$: | $\quad 2^{l - 1} \cdot t_{1}^{(n)} + (2^{l - 1} - 1) \cdot t_{2}^{(n)}\quad$ | $ t_1^{(r)} + (l - 1) t_{2}^{(r)}$ |
Table 1: Costs of Merkle-tree operations under single- and hybrid-hash strategies.
Depending on the exact native and in-circuit hashing times, it might be beneficial to resort to a different hashing strategy, such as using $C_1$ on the bottom two levels instead of the bottom one alone. In the extreme, this specialises back to the plain (i. e. single-hash) Merkle-tree construction where $C_1$ is used all throughout. Note that, in principle, nothing prevents one from using more than two different compression functions.
As an example, if $C_1$ is a bit-based hash which is essentially free compared to the arithmetic one $C_2$ (natively), switching to $C_1$ only at the bottom level would entail a ~50% performance improvement in the commitment phase. Using it at the last two levels instead would result in a ~66% improvement (but at the cost of a $2/l$ fraction of in-circuit hashing being affected, as opposed to $1/l$).
We stress that this trade-off only arises in the recursive setting: when performing direct, native verification, one should simply pick the fastest compression function.
Further notions
Although elegant and simple in abstract terms, Merkle trees involve a number of implementational decisions and admit many refinements and optimisations in various concrete settings. There is an interplay between these variants and the hybrid-hash strategy. Here are some further aspects of the construction to keep in mind:
Whereas the $\mathsf{Commit}$ method need only be called once, $\mathsf{Open}$ and $\mathsf{Verify}$ are often invoked multiple times (typically, as a way to increase the soundness of the overarching protocol). A large number of opening/verification calls would multiply the $1/l$ overhead (in the bottom-layer-only case) incurred by the switch to a bit-based hash, thus offseting the optimal equilibrium point for the hybrid strategy.
A frequent optimisation on Merkle trees are so-called caps. When capping the tree at the level $l’$, the prover only constructs levels $l$ through $l’$ of the tree instead of compressing further all the way to a single element. The commitment is therefore not one root of the form $r \in S$, but rather $2^{l’}$ caps $r_1, \ldots, r_{l’} \in S$. This technique increases the commitment size but saves verification work, which is reduced from $l$ calls to the compression function $C$ to $l - l’$ calls (leaving uncompressed, odd level-final nodes aside). As in the previous point, this alteration may affect the optimal balance between $C_1$ and $C_2$ in terms of both the choice of functions as well as how far up the tree to use $C_1$.
With the advent of single-instruction multiple-data (SIMD) chip architectures, bit-based hash functions may have even more of an edge over arithmetic ones by performing several operations in one processor cycle. On a related note, if one aims for a security level of 128 bits, tree nodes should be about 256 bits in size (recall that the birthday paradox implies that the probability of finding a collision of the hash function by brute force increases quadratically in the number of elements tested). However, not all operations of a 256-bit hash function such as SHA256 are performed on actual 256-bit vectors (which would indeed be larger than most chips’ registers).
A word of caution
We now briefly bring the reader’s attention to a potential pitfall when mixing hash functions as described above. So far we have assumed the usage of two compression functions $C_1, C_2 \colon S \times S \to S$. In practice, different hash functions often have different (co)domains - and crucially, this is necessarily the case when one of the two is bit-based and the other one, arithmetic. Let us therefore separate their domains and codomains and write $C_1 \colon S_1 \times S_1 \to S_1$ and $C_2 \colon S_2 \times S_2\to S_2$. In order to build a $(C_1, C_2)$-hybrid Merkle tree, one needs a conversion map $t \colon S_1 \to S_2$, which is applied to the last layer compressed with $C_1$ before proceeding with $C_2$. One should be wary of the interplay between $C_1$, $t$ and $C_2$ to avoid introducing vulnerabilities, in particular trivial ways to find collisions.
Note that, if the leaves being committed are field elements, switching to a bit-based hash $C_1$ also necessitates a conversion map $t’ \colon S_2 \to S_1$ in the other direction in order to transform those leaves into something $C_2$ can receive - however, simply expressing field elements as bit strings in any canonical way is typically safe.
2: An implementation
In a recent Plonky3 PR, we implemented a basic version of the hybrid-Merkle-tree concept. An important difference between the Plonky3 structure and plain Merkle trees is that the former is in actuality a multi-matrix commitment scheme (MMCS), which has two crucial features:
Each leaf is the digest (read: hash) of a certain row of a matrix $M$. More specifically, if the prover wants to commit to a matrix $M$ with $n = 2^l$ rows and an arbitrary number $c$ of columns, they first digest each row into a single field element and thus obtain a vector of $2^l$ field elements, which will constitute the leaves of the tree.
The tree is in fact a commitment to several matrices of varying sizes simultaneously. If the prover has, say, a matrix $M_1$ with $2^l$ rows as above, and another one $M_2$ with $2^{l - 1}$ rows (the number of columns is again irrelevant), they will first compress the leaves coming from $M_1$, obtaining $2^{l - 1}$ nodes $v_i^{(1)}$; and then add an injection step before compressing further. In this injection step, the $2^{l - 1}$ leaves coming from $M_2$ are interleaved with the $v_i^{(1)}$ and then pairwise compressed, forming an intermediate $2^{l - 1}$-node level. Many more details can be found in this fantastic post.
The aspect of MMCS most relevant to our discussion is that a substantial portion of the commitment and verification time is devoted not to compressing the leaves into a root, but rather to digesting potentially long matrix rows into leaves. Note that the amount of hashing needed to digest each row is the same for the prover and the verifier. In other words, the linear-vs-logarithmic asymmetry we exploited earlier is not present there and hence hybrid strategies are not such a good fit for the digestion phase.
We are now in a position to look at the generics of the plain Merkle-tree structure present in the original Plonky3 repository (source here):
pub struct MerkleTree<F, W, M, const DIGEST_ELEMS: usize> {..}
impl<F: Clone + Send + Sync, W: Clone, M: Matrix<F>, const DIGEST_ELEMS: usize>
MerkleTree<F, W, M, DIGEST_ELEMS>
{
pub fn new<P, PW, H, C>(h: &H, c: &C, leaves: Vec<M>) -> Self
where
P: PackedValue<Value = F>,
PW: PackedValue<Value = W>,
H: CryptographicHasher<F, [W; DIGEST_ELEMS]>,
H: CryptographicHasher<P, [PW; DIGEST_ELEMS]>,
H: Sync,
C: PseudoCompressionFunction<[W; DIGEST_ELEMS], 2>,
C: PseudoCompressionFunction<[PW; DIGEST_ELEMS], 2>,
C: Sync,
{..}
}
There is certainly quite a bit to take in, but the main ideas to keep in mind are:
Hrefers to the digestion function used to hash matrix rows into leaves.Crefers to the compression function used to go from leaves to a single root (as well as inject leaves corresponding to smaller-size matrices).- The reason each of
HandChas two hashing-related trait bounds is that the codebase takes advantage of SIMD-like capabilities and therefore includes code to hash packs of elements/nodes at once. This is what the second trait bound onHandCrefers to, with the first one being relating to single-element/node hashing.
As an example, C could be a Poseidon2 compressor over the BabyBear field, whose elements have 32 bits. If we want 256-bit nodes, a node must consist of 8 field elements. In terms of the generics, this would mean F = BabyBear, W = BabyBear and DIGEST_ELEMENTS = 8. Plonky3 offers instructions on packs of 4 BabyBear elements. This translates to packed nodes with 4 single nodes each, which in terms of generics means PW = PackedBabyBear: the implementation of PackedBabyBear: PackedValue<Value = Babybear> has associated constant WIDTH = 4. The trait bound C: PseudoCompressionFunction<[W; DIGEST_ELEMS], 2> means Poseidon2 must be able to compress two single leaves consisting of 8 BabyBear elements each, into one. The bound C: PseudoCompressionFunction<[PW; DIGEST_ELEMS], 2>, in turn, requires Poseidon2 to be able to compress pairs of packs of four leaves each (i. e. pairs of 32 BabyBear elements) into a single pack.
Although we will not delve into H because, as explained above, hybrid strategies have questionable applicability to the digestion phase, it is worth pointing out that when digesting a matrix of BabyBear (or any other type of) elements using the packed trait bound H: CryptographicHasher<P, [PW; DIGEST_ELEMS]>, each group of four (more generally: PW::WIDTH) rows is hashed in columnn-major order: the input to H is the sequence of four-element columns in the group of WIDTH of rows being digested.
Suppose now we wish to add hybrid-compression capabilities to the above structure. One natural choice would be to replace C by a pair of generics C1, C2 and use one or the other inside the new function (which performs the commitment algorithm) depending on the level being compressed (or injected). Instead, the chosen design replaces the trait bound on C by a new hybrid-compression trait which hides (almost) everything away from the MerkleTree structure. Where the original trait bound was defined as
pub trait PseudoCompressionFunction<T, const N: usize>: Clone {
fn compress(&self, input: [T; N]) -> T;
}
(with N = 2 in our case of interest), the new one looks as follows:
pub trait HybridPseudoCompressionFunction<T, const N: usize>: Clone {
fn compress(&self, input: [T; N], sizes: &[usize], current_size: usize) -> T;
}
In addition to the data to compress, the hybrid compression function receives size information about all levels of the tree, as well as which level it is being called at. It is then up to the implementor which compression function to use.
The new structure HybridMerkleTree has constructor trait bounds
pub fn new<P, PW, H, C>(h: &H, c: &C, leaves: Vec<M>) -> Self
where
P: PackedValue<Value = F>,
PW: PackedValue<Value = W>,
H: CryptographicHasher<F, [W; DIGEST_ELEMS]>,
H: CryptographicHasher<P, [PW; DIGEST_ELEMS]>,
H: Sync,
C: HybridPseudoCompressionFunction<[W; DIGEST_ELEMS], 2>,
C: HybridPseudoCompressionFunction<[PW; DIGEST_ELEMS], 2>,
C: Sync,
{...}
(source ).
We provide one implementor of HybridPseudoCompressionFunction: the simple strategy described above which uses $C_1$ to compress the bottom level and $C_2$ elsewhere. It should be noted that, since the MMCS protocol includes injection in addition to compression, $C_1$ is also used if there are matrices with (or: rounding up to) half the number of rows of those at the bottom level.
The SimpleHybridCompressor is defined as:
pub struct SimpleHybridCompressor<
// Compressor 1
C1,
// Compressor 2
C2,
// Node-element type for `C1`
W1,
// Node-element type for `C2`
W2,
// Number of elements of type `W1` that form a node
const DIGEST_ELEMS_1: usize,
// Number of elements of type `W2` that form a node
const DIGEST_ELEMS_2: usize,
// Node converter
NC,
> (..)
{
c1: C1,
c2: C2,
bottom_c1: bool,
(..)
}
The flag bottom_c1 indicates whether it is c1 or c2 that should be used at the bottom level (with the other one being used elsewhere). There are technical reasons why simply swapping the generics C1 and C2 does not achieve the same functionality.
When implementing the hybrid compression trait, we need to bound the input/output types of C1 and C2 to be convertible into one another:
impl<C1, C2, W1, W2, NC, const DIGEST_ELEMS_1: usize, const DIGEST_ELEMS_2: usize>
HybridPseudoCompressionFunction<[W1; DIGEST_ELEMS_1], 2>
for SimpleHybridCompressor<C1, C2, W1, W2, DIGEST_ELEMS_1, DIGEST_ELEMS_2, NC>
where
C1: PseudoCompressionFunction<[W1; DIGEST_ELEMS_1], 2> + Clone,
C2: PseudoCompressionFunction<[W2; DIGEST_ELEMS_2], 2> + Clone,
(..)
NC: NodeConverter<[W1; DIGEST_ELEMS_1], [W2; DIGEST_ELEMS_2]> + Clone,
{
fn compress(..) {..}
}
The trait NodeConverter<[W1; DIGEST_ELEMS_1], [W2; DIGEST_ELEMS_2]> to which NC is bound ensures the availability of functions to convert from [W1; DIGEST_ELEMS_1] to [W2; DIGEST_ELEMS_2] and viceversa. In the case of the SimpleHybridCompressor, if bottom_c1 is set to false (which should be the typical usage) conversion is only called once - from C1 to C2, after compressing the bottom level (and after injecting, if pressent at that level).
Several benchmarks, which can be found in merkle-tree/benches, accompany the implementation. Their differences and takeaways are described in more detail in the linked PR. We highlight hybrid_vs_plain_identity_hasher, which compares the prover costs when (natively) constructing a tree using a Poseidon2 compressor all throughout, versus a hybrid Blake3-Poseidon2 one. The “identity hasher” refers to the fact that the leaves fed to the tree are directly (packs of eight) field elements instead of hashes of longer matrix rows, thus removing digestion costs from the equation altogether.
Here is a snippet of the code that shows how cleanly hybrid trees can be constructed:
let h_identity = HIdentityBabyBear256 {};
let c_poseidon = poseidon2_compressor();
let c_blake3 = blake3_compressor();
let c_hybrid =
SimpleHybridCompressor::<_, _, _, _, 8, 32, UnsafeNodeConverter256BabyBearBytes>::new(
c_poseidon.clone(),
c_blake3.clone(),
false,
);
let leaves = get_random_leaves(NUM_MATRICES, MAX_ROWS, MAX_COLS);
(..)
HybridMerkleTree::new(&h_identity, &c_hybrid, leaves)
The time to commit to 200 matrices with a single column (to avoid digesting) and numbers of rows generated randomly between $1$ and $2^{15}$ is ~50 ms on a personal desktop computer with an i7-1165G7 processor and 32GB of RAM. Switching to the plain, Poseidon2-only tree results in a time of ~86 ms - which agrees with the expected ~50% time savings, taking into account that Blake3 has a negilible (native) cost compared to Poseidon2. We are glossing over many details here, including the fact that the numbers show less dramatic of an improvement on a different personal machine, as well as the inconvenient truth that using packed values (i. e. SIMD) on the plain, single-hash tree does yield a better performance than the single-value, hybrid tree described above (packed-value hybrid compression has not been implemented yet). Furthermore, the Plonky3 codebase does not have the arithmetic circuits necessary to test recursive verification times, which is naturally a key metric to take into consideration.
Many tasks remain on the horizon, such as improving on the design, handling node conversion better, adding packed-value hybrid-hashing capabilities and providing more implementors of the HybridPseudoCompression and NodeConverter traits. However, the existing code illustrates a reasonable approach to implmementing hybrid Merkle trees and should serve as an encouragement for more contributions to come.
Author: Antonio Mejías Gil